摄像机几何
将胶片直接放置在物体前方,胶片上的一个点会记录现实世界上的多个点,这样很难从胶片看到真实世界的,如下图所示。
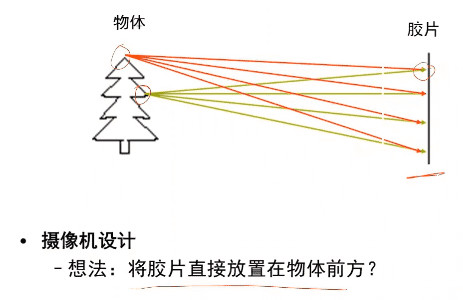
通过在胶片与现实世界中添加隔板,隔板上开个小孔,通过这个小孔可以使得胶片上的点与真实物体的点形成一一对应关系,如下图所示。

针孔摄像机的成像过程就是真实物体通过针孔在像平面形成像,如下图所示。其中小孔与像平面的距离就是焦距用$f$表示,小孔的大小就是光圈用$o$表示。
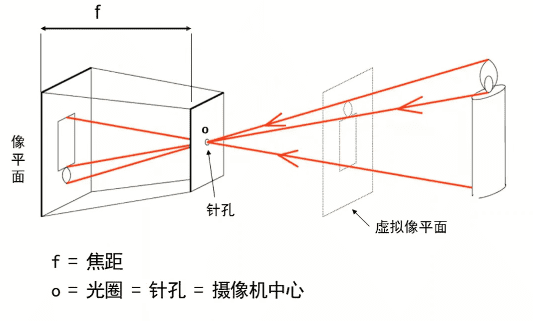
虚拟像平面与像平面对称,只不过方向相反。因为像平面与真实物体的z轴相反,在后面的推导中会忽略这个相反得z轴,假设推导的是虚拟像平面。
坐标系
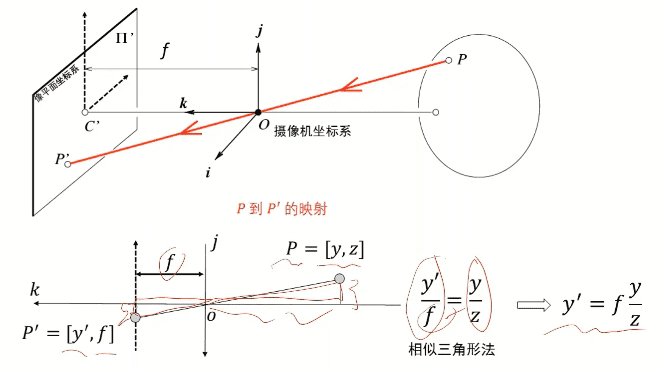
将真实物体点$P$到像平面点$P’$建立坐标系,如上图所示,关注$O,j,k$这个平面,真实点$P$与像平面点$P’$如一个相似三角形所示,根据相似三角形可以列出$y$与$y’$的关系表达式$: y’ = f\frac{y}{z}$,同理可以$x,z$的关系, $P = \begin{bmatrix}x\\ y\\ z \end{bmatrix} \to P’= \begin{bmatrix}x’ \\ y’ \end{bmatrix}$, $\begin{cases} x’=f\frac{x}{z} \\ y’ = f \frac{y}{z}\end{cases}$
通过这个转换就可以将空间点中的坐标转换到像平面上称为像平面上的坐标。因为图像仅表达二维信息,所以没有$z$轴的转换。
光圈与透镜

如图所示,随着光圈的缩小,成像越来越清晰,但亮度也越来越低,那是因为当光圈太大时,像平面上的一个点对应着真实物体的多个点,当缩小到合适的光圈时才会一一对应,随着光圈的缩小像平面的进光量也会减小,所以成像也就会越来越暗。为了增大进光量,可以在成像系统中加入透镜。
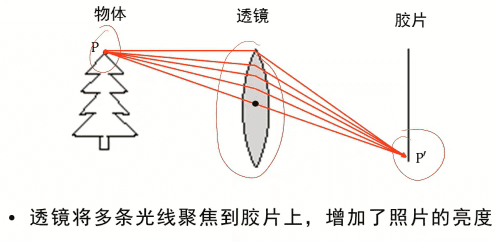
透镜将多条光纤聚焦到胶片上,增加了照片的亮度。
透镜的性质
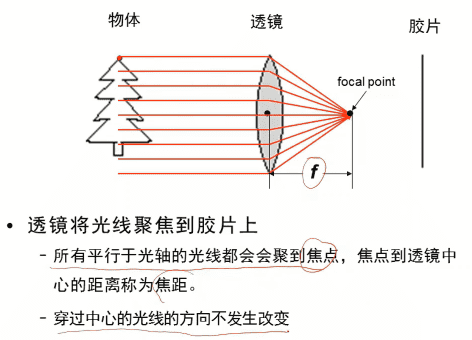
- 所有平行于光轴的光线都会聚集到焦点,焦点到透镜中心的距离称为焦距
- 穿过中心的光线的方向不发生改变
近轴折射模型
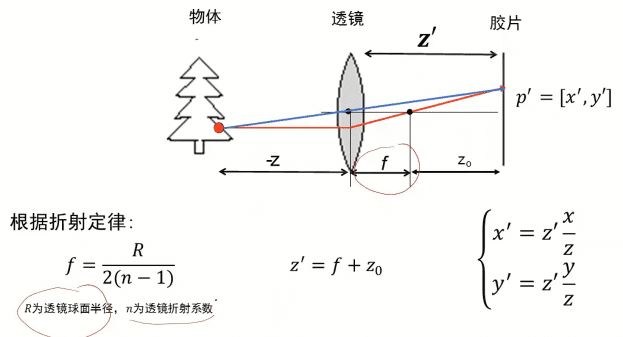
因为透镜的折射会聚焦到焦点$f$,所以针孔摄像机模型的焦距就记为$z’=f+z_0$,在透镜中只有经过小孔的点可以跟像平面上的点一一对应,所以这套系统仍然可以通过$\begin{cases} x’=f\frac{x}{z} \\ y’ = f \frac{y}{z}\end{cases}$来计算像平面与真实物体坐标之间的关系,只不过焦距中$f$变成了$z’$。
相机标定原理
- 空间无图表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型
- 这些几何模型参数就是相机参数
- 这个求解参数的过程就称之为相机标定
坐标系转换
相机坐标系到世界坐标系
世界坐标系
由于摄像机与被设想物体可以放置在环境中的任意位置,这样就需要在环境中建立一个坐标系,来表示设计摄像机和被摄物体的位置,这个坐标系就称为世界坐标系,世界坐标系通常是以物体中心为远点展开的。
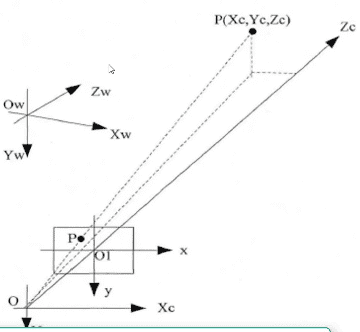
图中的$O_w,X_w,Y_w,Z_w$就构成了世界坐标系
相机坐标系
也是一个三维直角坐标系,原点位于镜头光心处,$x,y$轴分别与相面(摄像机的两边)的两边平行,$z$轴为镜头光轴,与相平面(摄像机的镜头平面)垂直。
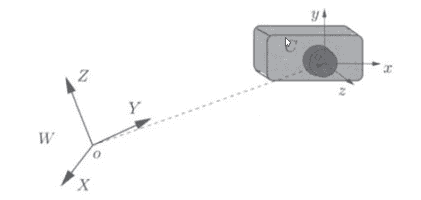
世界坐标系到相机坐标系的转换
旋转 :旋转矩阵,欧拉角,四元数,轴角,李群与李代数
根据线代知识,可以通过旋转矩阵来实现旋转。
$ \begin{bmatrix}X_c\\Y_c\\Z_c \end{bmatrix} = \begin{bmatrix}1 & 0 & 0\\0 & cos\theta & sin\theta \\ 0 & -sin\theta & cos\theta \end{bmatrix} \begin{bmatrix}X\\Y \\ Z \end{bmatrix}$, $\begin{cases} X_c = X \\ Y_c = cos\theta\cdot Y + sin\theta \cdot Z \\ Z_c = -sin \theta \cdot Y + cos\theta\cdot Z \end{cases}\ $
通过上面的转换可以将原本的坐标系按$X$轴旋转$\theta$度,得到一个新的坐标轴$X_c,Y_c,Z_c$
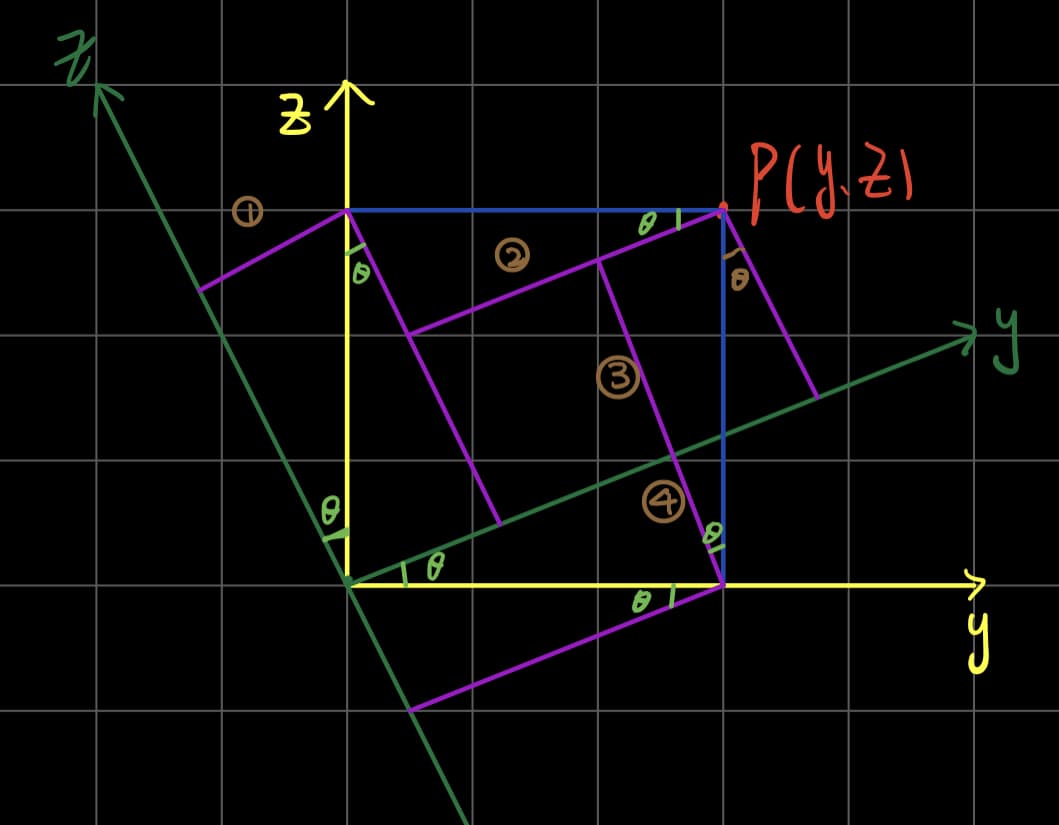
将$P$从原先的坐标系转换到新的坐标系,根据上图可以得到新的$y$是线1+线2,新的$z$是线3-线4
即新的坐标就是$\begin{cases} X_c = X \\ Y_c = cos\theta\cdot Y + sin\theta \cdot Z \\ Z_c = -sin \theta \cdot Y + cos\theta\cdot Z \end{cases}\ $
由绿色坐标系转向黄色坐标系则相反:$\begin{cases} X_c = X \\ Y_c = cos\theta\cdot Y - sin\theta \cdot Z \\ Z_c = sin \theta \cdot Y + cos\theta\cdot Z \end{cases}\ $
按照不同轴进行顺时针旋转的旋转矩阵如下:
- 沿$X$轴旋转:$R(X, \theta) = \begin{bmatrix}1 & 0 & 0\\0 & cos\theta & -sin\theta \\ 0 & sin\theta & cos\theta \end{bmatrix} $
- 沿$Y$轴旋转:$R(Y, \theta) =\begin{bmatrix} cos\theta & 0 & sin\theta\\0 & 1 & 0 \\ -sin\theta & 0 & cos\theta \end{bmatrix} $
- 沿$Z$轴旋转:$R(Z, \theta) =\begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0\\0 & 0 & 1\end{bmatrix} $
其中旋转角的正方向由右手螺旋定则给定,并且
将三个绕不同方向旋转的矩阵进行相乘
$[\sideset{^a}RPY{_B}(\phi, \theta, \psi)] = R(Z_A, \varphi)R(Y_A, \theta)R(X_A, \psi) \\ = \begin{bmatrix} c\varphi s\theta & c\varphi s\theta s\psi-s\varphi c\psi & c\varphi s\theta c\psi+s\varphi s\psi\\ c\varphi c\theta & s\varphi s\theta s\psi + c\varphi c\psi & s\varphi s\theta s\psi-c\varphi s\psi \\ -s\theta & c\theta s\psi & c\theta c\psi \end{bmatrix}$
左乘还是右乘
左乘: 相对于固定坐标系进行变换
$V’ = R \ast V = R_Z \ast R_Y \ast R_X V$
$(x_2, y_2)=A\ast (x_1, y_1)$
右乘:相对于自身(活跃)坐标系进行变换
$(x_2, y_2)=(x_1, y_1) \ast A$
世界坐标系到相机坐标系
$ \begin{bmatrix}X_c\\Y_c\\Z_c \end{bmatrix} = R \begin{bmatrix}X_W\\Y_W \\ Z_W \end{bmatrix}+T$,$R$是旋转矩阵,$T$是$X,Y,Z$轴方向的平移, $R,T$是相机的外参
即:$ \begin{bmatrix}r_{11} & r_{12} & r_{13}\\r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} \begin{bmatrix}X_W\\Y_W \\ Z_W \end{bmatrix}+\begin{bmatrix}t_x\\ t_y \\ t_z \end{bmatrix}$
将$R,T$合并成一个其次线性方程组
$ \begin{bmatrix}x_c\\y_c\\z_c \\ 1 \end{bmatrix} = \begin{bmatrix} R & t\\0 & 1\end{bmatrix}+\begin{bmatrix} x_w \\ y_w \\ z_w \\ 1\end{bmatrix}$
相机坐标系到图像坐标系
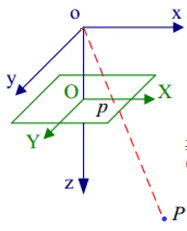
空间中任意一点$P$与其图像点$p$之间的关系,$P$与相机光心$o$的连线为$oP$,$oP$与像平面的交点$p$即为空间点$P$在图像平面上的投影。
该过程为透视投影,如下矩阵表示:
$ s\begin{bmatrix}X\\Y\\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0\\0 & f & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix}x \\ y\\ z \\ 1\end{bmatrix}$
其中,$s$为比例因子($s$不为0),$f$为有效焦距(光心到图像平面的距离),$(x, y, z,1)^T$是空间点$P$在相机坐标系$oxyz$中的齐次坐标$(X,Y,1)^T$是像点$p$在图像坐标系$OXY$中的齐次坐标。
$s$不是固定的,以$x$举例:$s X = fx, \frac{s}{f} = \frac{x}{X}, X = f\frac{x}{z}$,世界坐标系中的物体距离的远近会影响$s$的大小。
通过这样的转换,3维世界中的点可以转换到2维世界中,其中$x,y$经过转换成了新的坐标,$z$统一变成1,2维世界中不在有深度信息。
图像坐标系到像素坐标系转换
像素坐标系
- 像素坐标系$uov$是一个二维直角坐标系,反映了相机$CCD/CMOS$芯片中像素的排列情况
- 原点$o$位于图像的左上角,$u$轴、$v$轴分别于像面的两边平行
- 像素坐标系中坐标轴的单位是像素(整数)
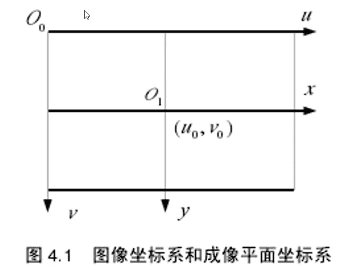
图像坐标系
- 像素坐标系不利于坐标变换,因此需要建立图像坐标系$XOY$
- 其坐标轴的单位通常为毫米(mm), 原点是相机光轴于相面的交点(称为主点),即图像的中心
- $X$轴,$Y$轴分别与$u$轴、$v$轴平行,故两个坐标系实际是平移关系,即可以通过平移就得到
图像坐标系转换为像素坐标系
$ \begin{bmatrix}u\\v\\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{dX} & 0 & u_0\\0 & \frac{1}{dY} & v_0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}X \\ Y \\ 1\end{bmatrix}$
其中,$dX$,$dY$ 分别为像素在$X、Y$轴方向上的物理尺寸,$u_0,v_0$为主点(图像原点)坐标
- $dX$的单位是$mm/$像素, $X$的单位是$mm$
世界坐标系转换成像素坐标系
$ s \begin{bmatrix}u\\v\\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{dX} & 0 & u_0\\0 & \frac{1}{dY} & v_0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} f & 0 & 0 & 0\\0 & f & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix} R & t\\0 & 1\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1\end{bmatrix}$
$= \begin{bmatrix} \alpha_x & 0 & u_0 & 0\\0 & \alpha_y & v_0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix} R & t\\0 & 1\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1\end{bmatrix} = M_1M_2X_w = MX_w$
$u = f_x\frac{X}{Z} +c_x, v = f_y \frac{Y}{Z}+c_y$
其中,$\alpha_x=\frac{f}{dX}, \alpha_y = \frac{y}{dY}$,$\alpha_x$也可以写成$f_x, s$称为$u,v$的尺度因子,$M_1$称为相机的内部参数矩阵,$M_2$称为相机的外部参数矩阵,$M$称为投影矩阵
畸变参数
- 在几何光学和阴极射线管(CRT)显示中,畸变是对直线投影的一种畸变
- 简单来说直线投影式场景内的以条直线投影到图片上也保持为一条直线
- 那畸变简单来说就是一条直线投影到图片上不能保持一条直线了,这时一种光学畸变
- 畸变一般分为两大类,包括径向畸变和切向畸变,主要的一般径向畸变有时也会有轻微的切向畸变
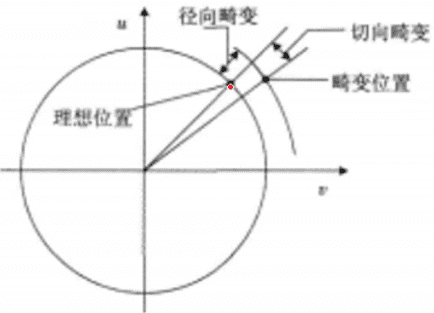
径向畸变
- 实际摄像机的透镜总是在成像仪的边缘产生显著的畸变,这种现象来源于“筒形”或“鱼眼”的影响
- 光纤在原理透镜中心的地方比靠经中心的地方更加弯曲,对于常用的普通透镜来说,这种现象更加严重
- 对于径向畸变,成像仪中心(光学中心)的畸变为0,随着向边缘移动,畸变越来越严重
切向畸变
- 切向畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的
- 切向畸变可分为:薄透镜畸变、离心畸变
畸变矫正
- 径向畸变矫正公式:$\begin{cases} x_{corr} = x_{dis}(1+k_1r^2+k_2r^4+k_3r^6) \\ y_{corr}= y_{dis}(1+k_1r^2+k_2r^4+k_3r^6) \end{cases}\ $
- 切向畸变矫正方式:$\begin{cases} x_{corr} = x_{dis}(2p_1xy+p_2(r^2+2x^2)) \\ y_{corr}= y_{dis} + [p_1(r^2+2y^2)+2p_2xy] \end{cases}\ $
其中,$x_dis$和$y_dis$表示有畸变的坐标,$x_{corr}$和$y_{corr}$表示修复后的坐标,$k_1,k_2,k_3$表示径向畸变参数,$p_1,p_2$表示切向畸变参数
张氏标定法
标定参考物
标定参考物一般都是棋盘,棋盘是一块黑白方块间隔组成的标定板,我们用它作为相机标定的标定物(从真实世界映射到数字图像内的对象)。之所以我们用棋盘作为标定物是因为平面棋盘模式更容易处理(相对于复杂的三维物体),但与此同时,二维物体相对于三维物体会缺少一部分信息,于是我们会多次改变棋盘的方位来捕获图像,以获得更丰富的坐标信息。
因为世界坐标系是人为定义的,所以我们可以假设标定棋盘位于世界坐标系中$Z_w=0$的平面,这时原矩阵
$s \begin{bmatrix}u\\v\\ 1 \end{bmatrix} = \begin{bmatrix} \alpha_x & 0 & u_0 & 0\\0 & \alpha_y & v_0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix} R & t\\0 & 1\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1\end{bmatrix}$ 就可以写成$\begin{bmatrix}u\\v\\ 1 \end{bmatrix} = s\begin{bmatrix} f_x & \gamma & u_0 \\0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} r_1 & r_2 & t\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ 1\end{bmatrix}$,其中$\gamma$是畸变参数
单应性变换
来描述物体在世界坐标系和像素坐标系之间的位置映射关系,对应的变换矩阵称为单应性矩阵。在上述式子中,单应性矩阵定义为:
$H=s\begin{bmatrix} f_x & \gamma & u_0 \\0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} r_1 & r_2 & t\end{bmatrix} = s M \begin{bmatrix} r_1 & r_2 & t\end{bmatrix}, M = \begin{bmatrix} f_x & \gamma & u_0 \\0 & f_y & v_0 \\ 0 & 0 & 1\end{bmatrix}$
估计单应性矩阵
首先单应性矩阵可以写成这样:$H= \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}$
我们假设两张图像中的对应点对对齐次坐标为$(x’,y’,1)$和$(x,y,1)$,那么:$\begin{bmatrix} x’ \\ y’ \\ 1 \end{bmatrix} \sim \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
展开后:$x’ = \frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h{33}} \\ y’ = \frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h{33}}$
由于齐次方程组乘上一个非零常数$k$并不改变结果,比如$x’ = \frac{kh_{11}x+kh_{12}y+kh_{13}}{kh_{31}x+kh_{32}y+kh{33}} \\ y’ = \frac{kh_{21}x+kh_{22}y+kh_{23}}{kh_{31}x+kh_{32}y+kh{33}}$, 所以对于最终的结果常量$h_{33}$我们可以将其乘上一个$k$使其为1,与之对应的其他参数也会乘上$k$。简单来说,不管最终求出来的$h_{33}$是多少,都会有一个$k$使其变成1,那么我们就消除了一个自由度,只剩下8个未知量。
化简$x’,y’$:$(h_{31}x+h_{32}y+h_{33})x’ = h_{11}x + h_{12}y + h_{13} \\ (h_{31}x + h_{32}y + h_{33})y’ = h_{21}x + h_{22}y + h_{23}$ $\to$ $h_{11}x + h_{12}y + h_{13} - h_{31}xx’-h{32}yx’-h_{33}X’ = 0\\ h_{21}x + h_{22}y + h_{23} - h_{31}xy’ - h_{32}yy’-h_{33}y’ = 0$
写成矩阵形式:$\begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1x_1’ & -y_1x_1’ & -x_1’ \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -x_1y_1’ & -y_1y_1’ & -y_1’ \\ \\ \\ \\ \\ \\ \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \\ \\ \\ \\ \\ \\ \end{bmatrix}$
因为已经确定了一个参数,所以只需要确定4个点就可以解出剩余的8个未知量



