所谓信息就是所获得的新知识,信心是用来减少随即不确定性的东西
— 信息论创始人香农
信息的量化
信息量的计算式可表示为:
$I(x_k)= \log_2\frac{1}{p_k}=-\log_2p_k$
其中$p_k$是时间$x_k$发生的概率,从概率信息定义可知:概率小$\to$信息量大,即信息量是发生概率的单调递减函数,此外,该定义也体现了信息量具有可加性。
自信息
定义
若一随机时间的概率为$p(x_i)$,它的自信息的数学定义为:$I(x_i)=f(p(x_i))=-\log p(x_i)$
$f(\cdot)$表示信息测度,表明自信息是事件概率的函数
性质
- 非负
- 单调递减
- 当$p(x_i)=0$时,$I(x_i)\to 0$,不可能事件
- 当$p(x_i)=1$时,$I(x_i)\to 0$, 确定事件
自信息量$I(x_i)$的含义
当事件$x_i$发生以前,表示事件$x_i$发生的不确定性
当事件$x_i$发生以后,表示事件$x_i$所提供的信息量
联合自信息量定义
二维联合集$XY$上的元素$(x_iy_i)$的联合自信息量定义为:$I(x_iy_j)=-\log p(x_iy_j)$
其中, $p(x)=\begin{equation} \left[ \begin{array}{lr} XY \\ P(XY)\end{array} \right] \end{equation} = $ $\begin{equation} \left\{ \begin{array}{lr} x_1y_1, \cdots, x_1y_m, x_2y_1, \cdots, x_2y_m, \cdots, x_ny_1, \cdots, x_ny_m \\ p(x_1y_1), \cdots, p(x_1y_m), p(x_2y_1), \cdots, p(x_2y_m), \cdots, p(x_ny_1), \cdots, p(x_ny_m) \end{array} \right\} \end{equation},$ $0 \le p(x_iy_i) \le 1, \sum\limits_{i=1}^n \sum\limits_{j=1}^{m}p(x_iy_j)=1$
条件自信息量定义
二维联合集$XY$中,对事件$x_i$和$y_j$,事件$x_i$在事件$y_j$给定的条件下的条件信息量定义为:$I(x_i/y_j)=-\log_2 p(x_i/y_j)$
关系
$I(x_iy_j)=-\log p(x_i) p(y_j/x_i)=I(x_i)+I(y_j/x_i)$
$= -\log_2 p(y_j)p(x_i/y_j) = I(y_j)+I(x_i/y_j)$
当$X$和$Y$独立时,$I(x_iy_j)=-\log_2 p(x_i)-\log_2 p(y_j) = I(x_i)+I(y_j)$
互信息
- 信源发出信息$x_i$的概率$p(x_i)$称为 先验概率,信宿收到$y_j$后推测信源发出$x_i$的概率$p(x_i/y_j)$称为 后验概率
- 由于有信道噪声的存在,一般情况下,$p(x_i/y_j)$不等于$p(x_i)$
互信息定义
定义$x_i$的后验概率与先验概率比值的对数为$y_j$对$x_i$的 互信息 , 用$I(x_i;y_j)$表示,即
$I(x_i; y_j)=\log_2 \frac{p(x_i/y_j)}{p(x_i)}, (i = 1, 2, \cdots, n; j = 1, 2, \cdots, m)$
互信息等于自信息减去条件自信息
$I(x_i; y_j) = -\log_2 p(x_i) + \log_2 p(x_i/y_j) = I(x_i) - I(x_i/y_j)$
第三种表达方式:
$I(x_i; y_j) = I(x_i)+I(y_j) - I(x_iy_j)$
物理意义
- $I(x_i;y_j) = I(x_i)-I(x_i/y_j)$
- 自信息$I(x_i)$ — 信宿收到$y_j$以前,对信源发$x_i$的不确定度
- 条件自信息$I(x_i/y_j)$ — 信宿收到$y_j$之后,对信源发$x_i$的不确定度
- 互信息$I(x_i;y_j)$ — 收到$y_j$而得到(关于$x_i$)的互信息,为不确定度的减少量
性质
互易性: $I(x_i;y_j) = I(y_j;x_i)$
当事件$x_i$与$y_j$统计独立时,互信息为零, 即$I(x_i;y_j)=0$
互信息可正可负
任何两事件之间的互信息不可能大于其中任意事件的自信息:
$I(x_i; y_j) \le I(x_i); I(x_i; y_j) \le I(y_j)$
条件互信息
定义
联合集$XYZ$中,给定条件$z_l$下,$x_i$与$y_j$之间的互信息,其定义式为
$I((x_i;y_j)/z_l)= I(x/z) - I((x/y)z) = \log \frac{p(x_i/y_jz_l)}{p(x_i/z_l)}$
推论1: $I(x_i;y_jz_l)=I(x_i;z_l) + I(x_i; y_j/z_l)$
推论2: 对于任意三个离散随机事件$x, y$和$z$存在着下列关系
$I(x;y/z)-I(x;y) = I(y;z/x)-I(y;z) = I(z;x/y)-I(z;x)$
平均自信息量(信源熵)
自信息是一个随机事件概率的函数,不能用作整个信源的信息测度。为了研究整个事件集合或符号序列(如信源)的平均的信息量(总体特征),
就需要引入新的概念,从数学上看是 数学期望,定义自信息的数学期望为信源的平均信息量,称为信源的平均自信息量(信源熵):
$H(X) = E[I(a_i)] = \sum\limits_{i=1}^n p_iI(a_i) = -\sum\limits_{i=1}^n p_i \log p(a_i)$ ,单位$\mathbb{bit}/$(信源) 符号
这个平均自信息量的表达式和统计物理学中的热熵的表达式很相似,在统计物理学中,热熵是一个物理系统杂乱性(无序性)的度量。
这在概念上也有相似之处,因此就借用“熵”这个词把平均自信息量$H(X)$称为“信源熵”。
信息熵具有一下三种物理含义
- 表示信源输出前,信源的平均不确定性
- 表示信源输出后,每个符号所携带的平均信息量
- 反映了变量$X$的随机性
联合熵
联合离散符号集合$XY$上的每个元素对$x_i, y_j$的联合自信息量的数学期望
$H(XY)=\sum\limits_{i=1}^n \sum\limits_{j=1}^m p(x_iy_j)I(x_iy_j) = - \sum\limits_{i=1}^n \sum\limits_{j=1}^m p(x_iy_j) \log_2 p(x_iy_j)$
条件熵
在联合符号集合$XY$上的条件自信息量的数学期望,在已知随机变量$X$的条件下,随机变量$Y$的条件熵定义为:
$H(Y/X) = E[I(y_j/x_i)] = \sum\limits_{j=1}^m \sum\limits_{i=1}^n p(x_iy_j) I(y_j/x_i) = -\sum\limits_{j=1}^m \sum\limits_{i=1}^n p(x_iy_j)\log_2 p(y_j/x_i)$
熵函数
$H(X)=H(p_1,p_2,\cdots,p_n) = -\sum\limits_{i=1}^n p_i \log p_i, \sum\limits_{i=1}^n p_i = 1, p_i \ge 0 (i = 1, 2, \cdots, n)$
二元熵: $H(X) = H(p, 1-p) = H(p)$
对称性
$H(p_1, p_2, \cdots, p_n) = H(p_n, p_1, p_2,\cdots, p_{n-1})$
根据加法交换律可以证明,当变量交换顺序时熵函数的值不变。信源的熵只与概率空间的总体结构有关,而与单个概率分量对应的状态顺序无关。
非负性
$H(X)\ge 0$
扩展性
$\mathbb{Lim}_{\epsilon \to 0} H_{n+1} (p_1, p_2, \cdots, p_n-\epsilon, \epsilon) = H_n(p1, P_2, \cdots,p_n)$
信源空间中增加某些概率很小的符号,虽然当发出这些符号时,提供很大的信息量,但由于其概率接近于0,在信源熵中占极小的比重,并不影响信源的总体特征。
确定性
$H(1, 0) = H(0, 1) = H(1, 0, \cdots, 0) = 0$
当信源$X$的信源空间$[X, P]$, 任一概率分量等于1,根据完备空间特性,其他概率分量必为0, 这时信源为一个确定信源,其熵为0。 此时,这个信源没有不确定性,信源输出符号后不提供任何信息量。
可加性
$H(XY) = H(X) + H(Y/X) \\ H(XY) = H(Y) + H(X/Y)$
- 可加性是熵函数的性质中最重要的一条性质,此性质的物理含义为知识的可积累性
- 可加性表明任何复杂问题,都可以分布解决,即对于某一事物存在的不确定度,如果无法一步完全解除,则可分布解除。
极值性
$H_n(p_1, p_2, \cdots, p_n) \le \log n$
上式表明,对于具有$n$个符号的离散信源,只有在$n$个信源符号等可能出现的情况下,信源熵才能达到最大值,这也表明等概分布的信源的平均不确定性最大,这是一个很重要的结论,称为 最大离散熵定理
推论1: 任何概率分布下的信息熵一定不会大于它对其他概率分布下自信息的数学期望
$H_n(p_1,p_2,\cdots,p_n) \le - \sum\limits_{i=1}^n p_i \log q_i \\ where: \sum\limits_{i=1}^n p_i = \sum\limits_{i=1}^n q_i = 1\ and \ p_i, q_i \ge 0$
推论2: 条件熵一定不会大于无条件熵,即$H(X) \ge H(Y/X)$
上凸性
设$f(x)=f(x_1,x_2,\cdots, xn)$为一多元函数。若对于任意一个小于1的正数$\alpha(0\lt \alpha \lt 1)$以及函数$f(X)$定义域内的两个任意矢量$X_1, X_2$有
$f[\alpha X_1+(1-\alpha)X_2] \ge \alpha f(X_1) + (1 - \alpha) f(X_2)$
则称$f(X)$为定义域上的上凸函数。
- 若$”=”$不成立,则为严格上凸函数
- 若$”\le”$则为下凸函数
- 若$”\lt”$ 则为严格下凸函数
由于熵函数具有上凸性,熵函数必有最大值
熵函数之间的互换关系
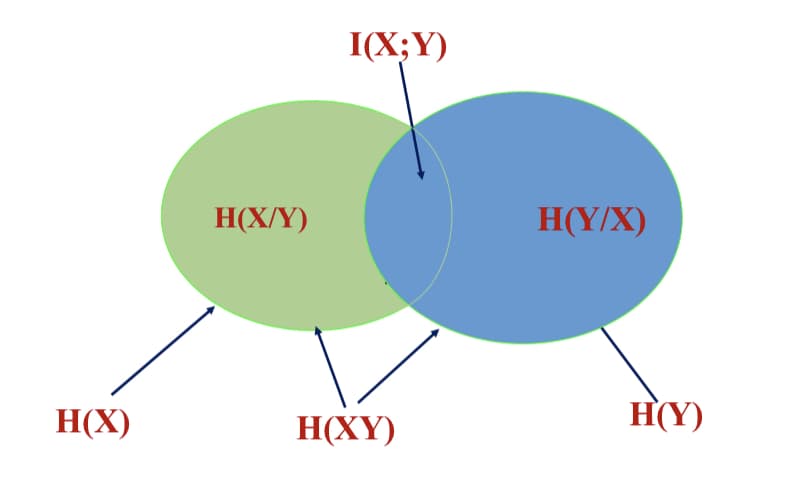
联合熵与信息熵、条件熵的关系
$H(XY) = H(X) + H(Y/X) = H(Y) + H(X/Y)\\ H(XY) \le H(X) + H(Y) \\ H(X/Y) \le H(X), H(Y/X) \le H(Y)$
等号成立的条件是$X$与$Y$相互独立
熵函数的可加性推广
$H(X_1, X_2, \cdots, X_N) = H(X_1) + H(X_2/X_1) + H(X_3/X_1X_2)+\cdots + H(X_N/X_1X_2\cdots X_{N-1}) \\ = \sum\limits_{i=1}^N H(X_i/X_1X_2\cdots X_{i-1})$
$H(X_1X_2\cdots X_N) \le H(X_1) + H(X_2) + \cdots + H(X_N)$
从信息传输系统角度看熵的意义
- $H(X)$:表示信源边每个符号的平均信息量(信源熵)
- $H(Y)$:表示信宿边每个符号的平均信息量(信宿熵)
- $H(X|Y)$:条件熵$H(X/Y)$表示在信宿接收到$Y$后,信源$X$尚存的平均不确定性。这个对$X$尚存的不确定性是由于信道干扰引起的,有时称$H(X/Y)$为信道疑义度,也称损失熵
- $H(Y|X)$:噪声熵,表示在已知信源发出$X$后,对于信宿$Y$尚存的平均不确定性,这是由于噪声引起的,也叫噪声熵
- $H(XY)$:表示整个信息传输系统的平均不确定性
平均互信息
互信息量$I(x_iy_j)$ 是定量地研究信息流通问题的重要基础,但它只能定量地描述输入随机变量发出某个具体消息$x_i$,输出变量出现某一个具体消息$y_j$时,流经信道的信息量;此外$I(x_iy_j)$还是随$x_i$和$y_j$变化而变化的随机变量,不能从整体上作为信道中信息流通的测度。这种测度应该从整体的角度出发,在平均意义上度量每通过一个符号流经信道的平均信息量。
定义
在联合概率空间$P(XY)$中,统计平均值为$Y$对$X$的平均互信息量为:
$I(X;Y)=\sum\limits_{j}\sum\limits_{i} p(x_iy_j)I(x_i;y_j) = \sum\limits_{j}\sum\limits_{i}p(x_iy_j)\log \frac{p(x_i/y_j)}{p(x_i)}$
与其他熵的关系
- $I(X;Y)=H(X)-H(X/Y)$ $H(X)$ 表示传输前信源的不确定性,而$H(X/Y)$表示收到符号集合$Y$后,对信源$X$尚存的不确定性,所以二者之差为信道传递的平均信息量
- $I(X;Y)=H(X)-H(Y/X)$ $I(X;Y)$ 也表示输出端$H(Y)$的不确定性和已知$X$的条件下关于$Y$的不确定性之差,也等于发送前后关于$Y$的不确定性之差。
- $I(X;Y)=H(X)+H(Y)-H(XY)$
- $I(X;Y)$ 确定通过信道的信息量的多少,因此称它为信道传输率或传信率
学习要点
自信息: $I(a_i) = -\log p_i$
自互信息: $I(a_i;b_j) = \log \frac{P(a_i/b_j)}{p(a_i)} = I(a_i) - I(a_i/b_j)$
信息熵: $H(X) = E[I(a_i)] = -\sum\limits_{i=1}^n p_i \log p_i$
联合熵: $H(XY) = \sum\limits_{i=1}^n \sum\limits_{j=1}^m p(x_iy_j)I(x_iy_j) = -\sum\limits_{i=1}^{n}\sum\limits_{j=1}^m p(x_iy_j)\log_2p(x_iy_j)$
条件熵: $H(Y/X) = E[I(y_j/x_i)] = \sum\limits_{j=1}^m \sum\limits_{i=1}^n p(x_iy_j)I(y_j/x_i) = -\sum\limits_{j=1}^m \sum\limits_{i=1}^n p(x_iy_j) \log p(y_j/x_i)$
熵函数性质:
- 对称性: $H(p_1,p_2,\cdots,p_n) = H(p_2, p_1, \cdots, p_n)$
- 非负性:$H(X)\ge 0$
- 扩展性:$\lim \limits_{\epsilon \to 0} H_{n+1}(p_1, p_2, \cdots, p_n, \epsilon)=H_n(p_1, p_2,\cdots, p_n)$
- 确定性:$H(1, 0) = H(1, 0, 0) = H(1,0,0,\cdots, 0)=0$
- 可加性:$H(XY) = H(X)+H(Y/X)$
- 极值性:$\log n = H_0 \ge H_1 \ge \cdots H_{\infty}$
- 上凸性:$H[\theta P_i + (1-\theta)Q_i] \ge \theta H(P_i) + (1-\theta)H(Q_i)$
联合熵与信息熵、条件熵的关系:
$H(X/Y) \le H(X), H(Y/X) \le H(Y), H(XY) \le H(X) + H(Y)$
$H(XY) = H(X) + H(Y/X) = H(Y) + H(X/Y)$
平均互信息: $I(X;Y) = \sum\limits_{j} \sum\limits_{j} p(x_i y_j) I(x_i; y_j)= \sum\limits_{j}\sum\limits_{i} p(x_i y_j) \log \frac{p(x_i/y_j)}{p(x_i)}$
平均互信息与各类熵之间的关系: $I(X;Y) = H(X)-H(X/Y)=H(Y)-H(Y/X)=H(X)+H(Y)-H(XY)$
信息散度: $D(P//Q) = \sum\limits_{X} P(x) \log \frac{P(x)}{Q(x)}$
数据处理定理:
$I(X;Z) \le I(Y;Z), I(X;Z) \le I(X;Y)\\ I(X;Y_1) \le I(X;Y_1Y_2)\le \cdots \le I(X; Y_1\cdots Y_m)$
序列熵、平均符号熵和极限熵:
$H(\vec{X}) = H(X_1 X_2\cdots X_L) = - \sum\limits_{i_1}\sum\limits_{i_2}\cdots \sum\limits_{i_L} P_{i_1i_2\cdots i_L} \log P_{i_1i_2\cdots i_L} $
$H_L(\vec{X}) = \frac{1}{L} H(X_1 X_2\cdots X_L)$
$H_{\infty} (\vec{X}) = H_{\infty} = \lim\limits_{L\to \infty} \frac{1}{L} H(\vec{X}) = \lim\limits_{L\to \infty} H(X_L / X_{L-1} X_{L-2} \cdots X_{L-m})$
马尔可夫信源:
$H(X_L/X_{L-1} X_{L-2} \cdots X+1) = H(X_L / X_{L-1} X_{L-2} \cdots X_{L-m})$
$H_{\infty} = -\sum\limits_{i=1}^n \sum\limits_{j=1}^n \pi_i P_{ji} \log P_{ji}, pi_i \in \{\pi_1, \pi_2,\cdots,\pi_{n^L} \}$为极限分布
近似马尔可夫信源:
$H_{m+1}=\lim \limits_{L\to \infty} H(X_L/X_{L-1}\cdots X_{L-m})$
$\log n = H_0 \ge H_1 \ge \cdots H_{\infty}$