代价函数
神经网络

使用$L$来代表神经网络的层数
使用$s_l$来代表第$l$层的神经元数目
代价函数

相对于单个的逻辑回归的代价函数,整个神经网络的代价函数只对输出层进行计算,计算第$i$的输出与训练集的结果$y_i$之间的差距。因为神经网络的数据不是唯一,可能由多个分类的输出,所以$K$代表输出的分类个数。计算正则化也是如何,跟逻辑回归类似,不计算0下表的$\Theta$
反向传播算法
向前传播方法
向前传播方法是前面用到的方法
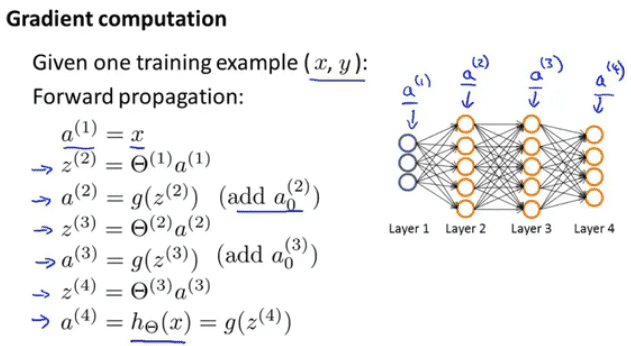
从输入开始,对每一层进行计算得到下一层的结果,以此往复得到最终结果
反向传播方法
方向传播方法从直观上说就是对每一个节点计算$\delta_j^{(l)}$代表第$l$层,第$j$个节点的误差

还是使用4层的神经网络来说
$\delta_j^{(4)}=a_j^{(4)}-y_j$
第四层就是输出值和$y$值的误差,然后我们反向传播到第三层
$\delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)} * g’(z^{(3)})$
$\delta^{(3)}$由参数$\Theta^{(3)}$转置叉乘$\delta^{(4)}$然后点乘(这里点乘只是各个数字相乘) $g(z^{(3)})$的导数,
对$g$函数求导,先设
$a = g(z) = \frac{1}{1+e^{-z}} $
$g’(z) \\ = (\frac{1}{1+e^{-z}})’ \\ = \frac{1’(\frac{1}{1+e^{-z}})+1(\frac{1}{1+e^{-z}})’}{(1+e^{-z})^2} \\ = \frac{e^{-z}}{(1+e^{-z})^2} \\ = \frac{e^{-z}+1-1}{(1+e^{-z})^2} \\ = \frac{(e^{-z}+1) -1}{(1+e^{-z})^2} \\ = \frac{1}{(1+e^{-z})}-\frac{1}{(1+e^{-z})^2} \\ = a - a^2 \\ = a(1-a)$
那么现在$g’(z^{(3)})$就为$a^{(3)}*(1-a^{(3)})$
同样的$\delta^{(2)}$也是如此
$\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)} * g’(z^{(2)})$
在不严谨的情况下,我们可以得到初略的偏导数$\frac{\partial}{\partial \Theta_{ij}^{(l)}}J(\Theta)=a_j^{(l)}\delta_i^{l+1}$ 这些都是忽略的正则化的情况下
反向传播算法

一开始我们将所有的$\Delta$设置为0,$\Delta$是$\delta$的大写形式
然后我们每一层计算$a^{l}$,计算到输出层以后倒回来计算$\delta$,一直计算到$\delta^2$
然后计算$\Delta$,$\Delta$的计算公式:$\Delta_{ij}^{(l)}:=\Delta_{ij}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}$
向量式写法可以写成$\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T$
最终计算$D$,$ \begin{array}{lr} D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)} & if\ j \not=0 \\ D_{ij}^(l) := \frac{1}{m}\Delta_{ij}^{(l)} & if\ j = 0 \end{array} $
这里加上了正则化
最终的偏导正好等于$\frac{\partial}{\partial \Theta_{ij}^{(l)}}J(\Theta)=D_{ij}^{(l)}$
理解反向传播算法
以单一的输出并且忽略$\lambda$为例,代价函数可以写成$cost(i)=y^{(i)}\log h_{\Theta}(x^{(i)})+(1-y^{(i)})\log h_{\Theta}(x^{(i)})$

最终的代价值是由每个节点的误差累计而成,所以对于最终的带价值,每一个$\delta_j^{(l)}$都相当于这个代价的偏导,由这些误差联合作用得到最终的误差值,而每一个$\delta_{i}^{(l)}$都可以从后面的$\delta$推导出来,比如$\delta_2^{2}=\Theta_{12}^{(2)}\delta_{1}^{(3)}+\Theta_{22}^{(2)}\delta^{(3)}_2$
这样就可以得出$\delta$的推导公式$\delta^{(l)}=(\Theta^{(l)})^T\delta^{(l+1)}$,至于那么求导暂时没搞懂
展开参数
假设一个神经网络第一层有10个节点,第二层有10个节点,第三层有1个节点
$s_1=10,s_2=10,s_3=1$
那么对应的参数就为
$\Theta^{(1)}\in\mathbb{R}^{10\times11},\Theta^{(2)}\in\mathbb{R}^{(10\times11)},\Theta^{(3)}\in\mathbb{R}^{(1\times11)}$
$D^{(1)}\in\mathbb{R}^{10\times11},D^{(2)}\in\mathbb{R}^{(10\times11)},D^{(3)}\in\mathbb{R}^{(1\times11)}$
$\Theta,D$都是矩阵,但是对于高级优化函数
$function\ [jVal,\ gradient] = costFunction(theta)\\ … \\ optTheta=fminunc(@costFunction, initialTheta, options)$
$theta, initialTheta, gradient$都是向量
所以这里就有一个向量展开的问题,通过操作将各个参数合并成一个向量
$thetaVec = [Theta1(:); Theta2(:);Theta3(:)];\\DVec=[D1(:);D2(:);D3(:)];$
在使用时再通过操作将向量转化成矩阵
$Theta1=reshape(thetaVec(1:110), 10,11);\\Theta2=reshape(thetaVec(111:220), 10,11);\\Theta1=reshape(thetaVec(221:231), 1,11);$
在使用高级优化函数时,也传入合并的向量
$fminunc(@costFunction,initialTheta,options)$
代价函数也有所改变
$function\ [jval,gradientVec]=costFunction(thetaVec)$
从$thetaVec$中获得$\Theta^{(1)},\Theta^{(2)},\Theta^{(3)}$,
通过反向传播算出$D^{(1)},D^{(2)},D^{(3)}$和$J(\Theta)$,再将矩阵转化成向量得到$gradientVec$
梯度检测
有时反向传播会出现一些我们发现不了的bug,而为了检测出这个bug,可以使用梯度检测的方法
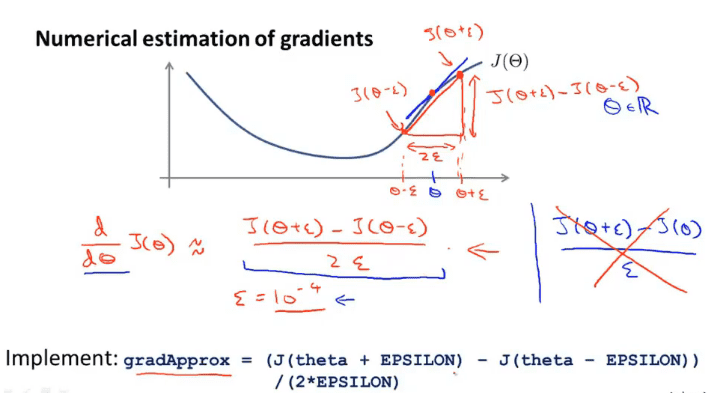
再常数的情况下,取一个很小的$\epsilon$,这样$\frac{d}{d\theta}J(\theta)\approx\frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\epsilon}$
在向量的情况下,每个偏导都计算一次,跟反向传播所计算出来的导数相比,就可以得出反向传播的正确率了

$for i = 1:n,$
$thetaPlus = theta;$
$thetaPlus(i) = thetaPlus(i) + EPSILON;$
$thetaMinus = theta;$
$thetaMinus(i) = thetaMinus(i) - EPSILON;$
$gradApprox(i) = (J(thetaPlus)-J(thetaMinus)) / (2*EPSILON)$
$end;$
检查是否$gradApprox\approx DVec$
如果跟$DVec$相差不是很大,那么就可以证明反向传播是正确的。
注意梯度检测只适用于检测阶段,是检测手段,不能再正式运行梯度下降时使用梯度检测,这会大大拖慢梯度下降的效率
随机初始化
在梯度下降算法中,需要初始化初始的参数,那么如何初始化呢。
对称权重
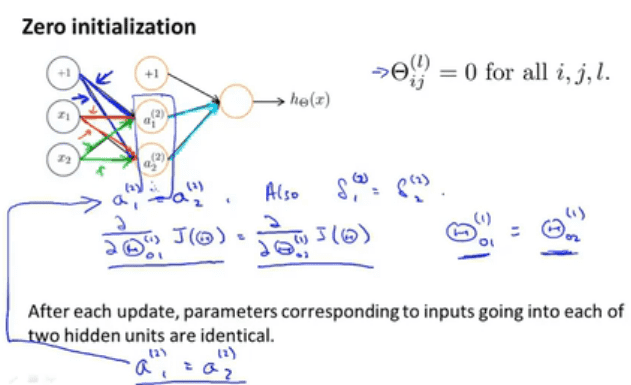
逻辑回归的初始化是将所有的参数设置成0,这样会造成一个问题,就是对称权重,每个输入值的权重相同,那么就导致隐藏层的值也相同,反馈到输出结果是造成每个隐藏层的$\delta$也相同,这也就意味着偏导数相同,对于隐藏层的一个节点,它的输入的边偏导相同时,无论经过多少次迭代,边始终都相同。$a^{(2)}_1,a^{(2)}_2$以相同的参数进行计算,它们始终相同。
所有的隐藏节点都在计算相同的特征,所有的隐藏单元都在以相同的函数作为输入,这是一种高度冗余的现象,因此这也意味着最终的输出单元,只能得到一种特征,因为所有的单元都一样。
随机初始化
随机初始化是解决对称权重的初始化方法。
随机初始化所有的$\Theta_{ij}^{(l)}$在$[-\epsilon,\epsilon]$之间
$Theta = ranf(10,11) \times (2 \times INIT_EPSILON) - INIT_EPSILON$
组合
选择神经网络结构
- 根据特征的维度确定输入单元个数
- 根据分类的需求确定输出单元个数
- 一般情况下隐藏层个数1个或者多个,每一层隐藏层单元数量个数相等,可以是输入单元的倍数
- 一般情况下,隐藏层个数越多越好,但是越多计算量越大
训练神经网络
- 构建神经网络,随机初始化权重
- 执行向前传播算法,根据输入的$x^{(i)}$计算输出值$h_{\Theta}(x^{(i)})$
- 通过代码计算代价函数$J(\theta)$
- 执行反向传播算法算出偏导数项$\frac{\partial}{\partial \Theta_{jk}^{(l)}}J(\Theta)$
- 使用梯度检测来检测已经计算出来的偏导数项,通过梯度检测方法可以保证我们反向传播得到的结果是正确的,然后停止梯度检测,因为梯度检测非常的慢
- 使用高级优化算法与反向传播算法结合



