神经网络
对于复杂的问题,由于特征值的数量增多,对于拟合出来的多项式复杂度可能会急剧膨胀,这样一来单独使用线性回归或逻辑回归可能就不太能满足需求了
神经元
神经元是神经网络里的一个运算单元,可以是线性回归,可以实逻辑回归或是其他算法,图中简单的表示对$h$函数做运算,$h_{\theta}(x)=\frac{1}{1+e^{-\theta^TX}}$ ,有输入$x_1,x_2,x_3$,有$x_0$没有绘出但是$x_0$存在且始终等于0,$x_0$称为偏移单元或偏移神经元。
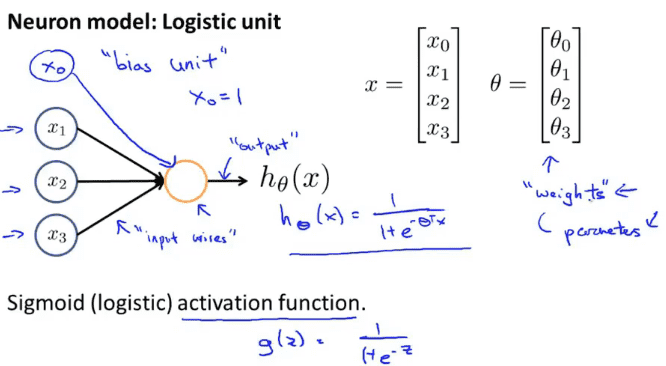
有时我们会说这是一个带有$Sigmoid$或者是$Logistic$激活函数的人工神经元,在神经网络的术语中,激活单元是指代非线性函数$g(z)=\frac{1}{1+e^{-z}}$的另一个术语
$\theta$在之前的描述种被称为模型的参数,在神经网络种有人会称它为模型的权重
神经网络
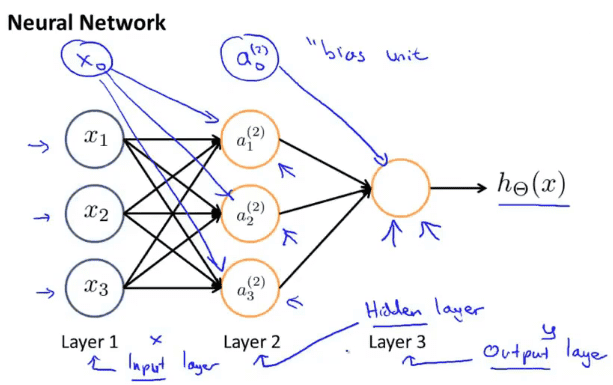
神经网络其实就是一组神经元链接在一起的集合,图中的神经网络输入$x_1,x_2,x_3$,当然有一个隐藏的$x_0$,$a_1^{(2)},a_2^{(2)},a_3^{(2)}$是3个神经元,并且有一个隐藏的神经元$a_0^{(2)}$,最后一层有一个输出节点假设函数$h_{\Theta}(x)$。
在神经网络的术语中第一层叫做输入层,最后一层叫做输出层,中间的叫做隐藏层
计算步骤
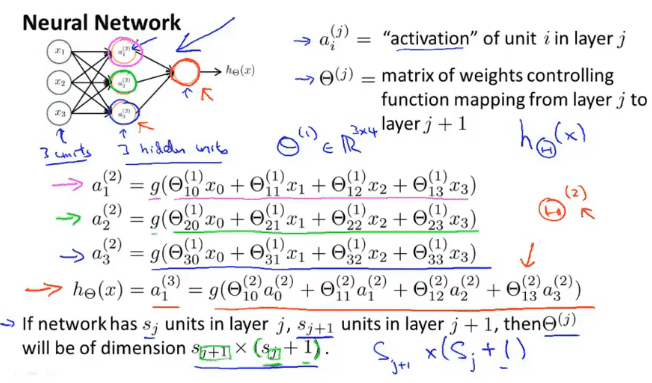
$a_i^{(j)}$代表第$j$层第$i$个神经元或单元
$\Theta^{(j)}$ 权重参数,控制从某一层到下一层的映射
从第一层的4个参数到第二层的3个神经元,通过$\Theta$来转换,$\Theta$的维度可以表示为$s_{j+1}\times (s_j+1)$
每一层的转换都是通过$\Theta$来实现,
向量化表示
仔细观察$x$向$z$转换的过程,我们将$x$组成一个向量,$z^{(2)}$来表示运算时$g$的参数,$z^{(2)}$的大小时$3\times 1$
$z^{(2)}$由$\Theta^{(1)}$与$a^{(1)}$矩阵相乘而来,$a^{(1)}$时输入的参数,加上隐藏的$x_0$的话,$a^{(1)}$的规格时$4\times 1$,以此类推,
计算$z^{(3)}$时,通过$\Theta^{(2)}$与$a^{(2)}$相乘就可以得到,而结果$h_{\Theta}(x)$就是$z^{(3)}$
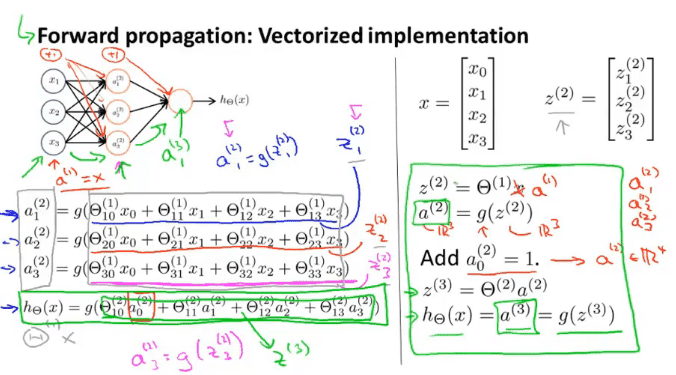
神经网络与常规的逻辑回归相比特殊之处在于,不直接使用输入的参数来计算结果,而是通过$\Theta$来计算中间隐藏层,通过隐藏层来计算最终结果
神经元计算样例
通过神经网络的一层层传递,我们可以在一些简单的计算的基础上再进行一些复杂计算,从而得到很好的计算结果
与运算
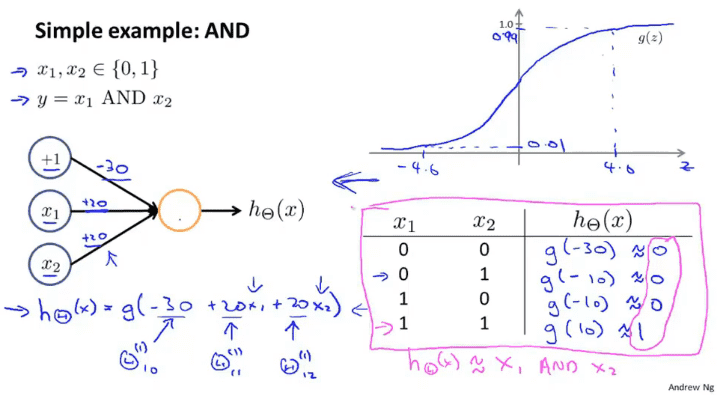
如图所示,我们设计设计一个神经元,将参数设置成$(-30,10,10)$,利用$g$函数可以达到与运算的效果
或运算

跟与运算相似,将参数设置成$(-10, 20, 20)$就可以达到或运算的效果
非运算
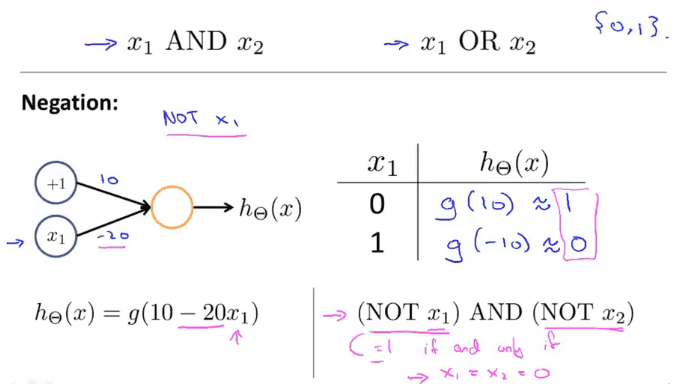
非运算,在需要运算的值前面加上一个很大的参数,就可以实现非运算了
异或运算

异或运算在中间的隐藏层实现与预算和非与运算来通过或运算得到异或运算,通过真值表可以看到正确性
多元分类
多元分类是在单元分类的基础上输出多个结果代表多个种类
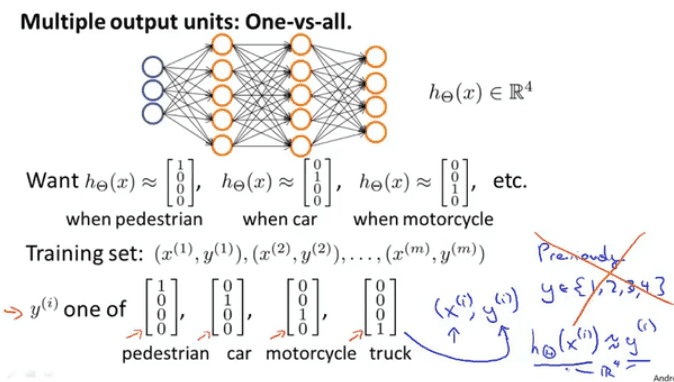
再多元分类中$y^{(i)}$不在代表一个值,而是一个向量,其中1的位置代表$y^{(i)}$的类型,我们要做的就是通过训练找到合适的$\Theta$,使得$h_{\Theta}(x^{(i)})\approx y^{(i)}$



