逻辑回归
二元分类
二元分类中$y$值只能取两个值,0或1
$y=\{ 0, 1\}$
一般的话,0代表没有,1代表有
逻辑回归
逻辑回归实际是一种分类算法,逻辑回归的输出值在0到1之间
$0\le h_{\theta}(x)\le1$
线性回归的一般公式是:$h_{\theta}(x)=\theta^Tx$,得到的是一个数值
而逻辑回归的公式则为:$h_{\theta}(x)=g(\theta^Tx)\\g(z)=\frac{1}{1+e^{-z}}$
$g$函数一般被称为 $sigmoid\ $函数或 $logistic\ $函数
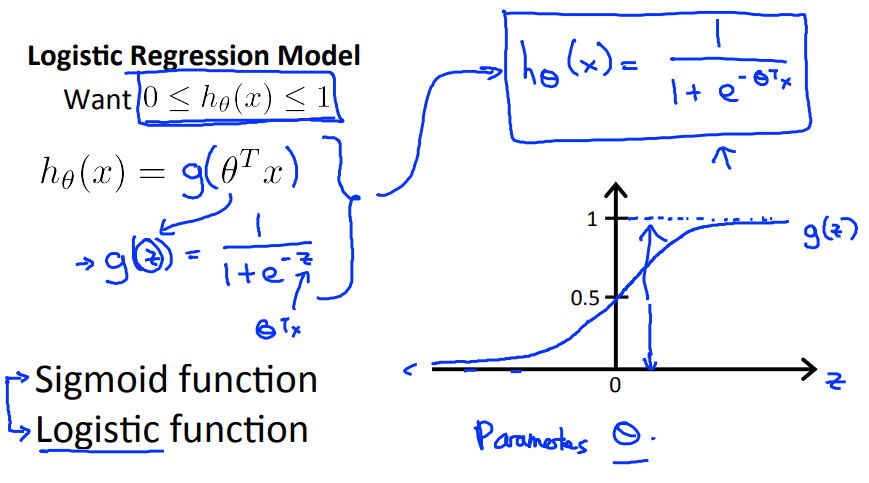
逻辑函数$h$的曲线在0到1之间,也可以说逻辑曲线的值参数$x$为1的可能性
$h_{\theta}(x)=p(y=1|x;\theta)$
在给定参数下,$h$函数判断同一数据为0的概率和为1的概率应该和是1
$P(y=0|x;\theta)+P(y=1|x;\theta)=1$
决策界限
根据上图所示,当$g$的参数$\ge0$时,$g$函数的值大于$0.5$,相应的当$g$的参数$\lt0$时,$g$函数的值小于$0.5$,而$g$函数的参数又是$\theta^TX$,所以我们可以得到结论当$\theta^TX\ge0$时,$h_{\theta}(x)\ge0.5$,当$\theta^TX<0$时,$h_{\theta}(x)>0.5$
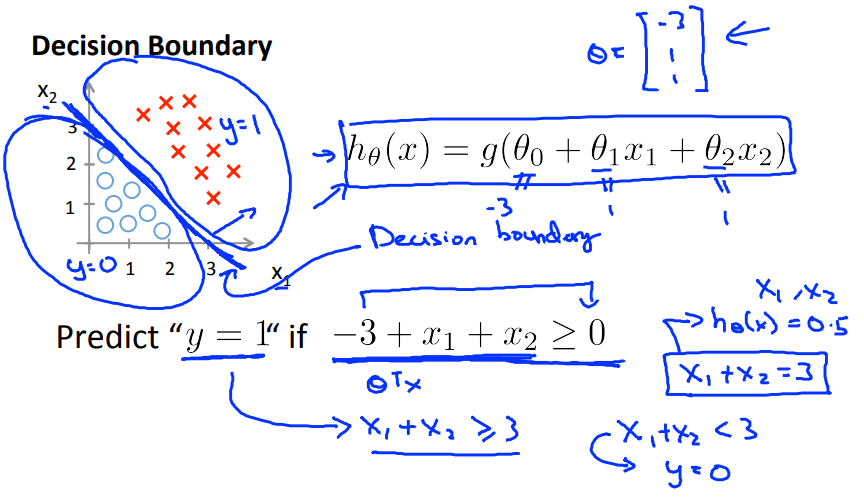
图上两种分类中间的直线就是决策界限
代价函数
原先的代价函数可以写成 $J(\theta)=Cost(h_{\theta}(x^{(i)}),y^{(i)})=\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2$
因为$h$函数是一个复杂的函数$h_{\theta}(x)=\frac{1}{1+e^{-\theta^Tx}}$,导致代价函数$J$是一个非凹函数,这样在梯度下降的过程中不一定会找到全局最小值
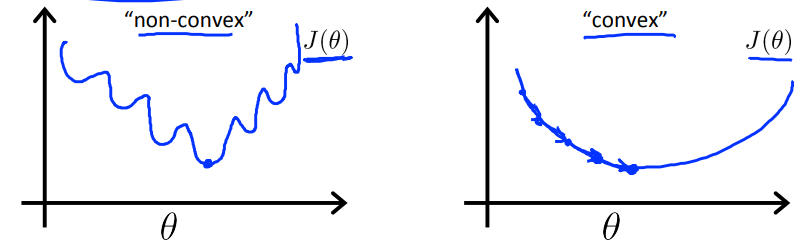
很显然这个代价函数并不适合逻辑回归,这里将介绍一个新的代价函数
$Cost(h_{\theta}(x),y) = \left\{ \begin{array}{lr} -\log(h_{\theta}(x)) & if\ y = 1 \\ -\log(1-h_{\theta}(x)) & if\ y = 0 \end{array} \right. $
当$y=1,h_{\theta}(x) =1$时$Cost$为0,如果$h_{\theta}(x)\to0$ ,那么$Cost\to \infty$
当$y=0,h_{\theta}(x)=0$时$Cost$为1,如果$h_{\theta}(x)\to1$,那么$Cost\to \infty$
简化代价函数
$J(\theta)=\frac{1}{m}\sum\limits_{i=1}^mCost(h_{\theta}(x^{(i)}), y^{(i)})$
$Cost(h_{\theta}(x),y) = \left\{ \begin{array}{lr} -\log(h_{\theta}(x)) & if\ y = 1 \\ -\log(1-h_{\theta}(x)) & if\ y = 0 \end{array} \right. $
因为代价函数中包括了两种不同的状态,不利于梯度下降函数的运行,所以我们要简化代价函数
$Cost(h_{\theta}(x),y) = -y \log(h_{\theta}(x)) - (1-y)\log(1-h_{\theta}(x))$
关于为什么要选择这个代价函数,我偶然看见一个UP做过一个视频,视频在这我简单说一下我的理解
因为神经网络的每次迭代都是通过改变$W,b$的值来实现,那么对于每一次训练我们来比较差错的话,就是在
当前$W,b$的情况下,去得到得出原本正确的$x_1,x_2,x_3…$的概率$P(x_1,x_2,…,x_n|W,b)$
因为神经网络得到的$y_i$跟$W,b$存在线性关系,所以还可以写成$\prod\limits_{i=1}^nP(x_i|y_i)$
神经网络算出的$y_i$的值只有01两种情况,所以这个式子还符合伯努利分布 :
$x_i\in{0,1}$
$f(x)=p^x(1-p)^{1-x}= \left\{ \begin{array}{lr} p, & x=1 \\ 1-p, & x=0 \end{array} \right. \ $
在伯努利分布中$p$代表为1的概率,而神经网络中的$y_i$也是为真的概率,那么方程就可以写成
$\prod\limits_{i=1}^ny_i^{x_i}(1-y_i)^{1-x_i}$,加上$log$变成加法
$\log(\prod\limits_{i=1}^ny_i^{x_i}(1-y_i)^{1-x_i}) \\ = \sum\limits_{i=1}^n \log(y_i^{x_i}(1-y_i)^{1-x_i}) \\ = \sum\limits_{i=1}^n (x_i \log y_i + (1-x_i) \log(1-y_i)) $
那么这里就是在当前迭代的情况下,最符合训练集的概率,这个公式是寻找最大值,所以加上负号变成
寻找最小值,以符合梯度下降,这就是逻辑回归的梯度下降
$Cost(h_{\theta}(x),y) = -y \log(h_{\theta}(x)) - (1-y)\log(1-h_{\theta}(x))$
这样我们就将两个式子简化成一行,新的代价函数为:
$J(\theta)=\frac{1}{m}\sum\limits_{i=1}^mCost(h_{\theta}(x^{(i)}), y^{(i)}) \\ = -\frac{1}{m}\sum\limits_{i=1}^m[y^{(i)}\log(h_{\theta}(x^{(i)}))+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))] $
我们利用梯度下降去寻找最小的$\min\limits_{\theta}J(\theta)$,去预测一个新的参数$x$为1的概率
梯度下降
逻辑回归的的梯度下降公式跟线性回归的几乎一样
$Repeat \{ \\ \theta_j:=\theta_j-\frac{\alpha}{m}\sum\limits_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j \\ \}$
向量式写法:
$\theta := \theta - \frac{\alpha}{m}X^T(g(X\theta)-y)$
高级优化
Octave中有许多由于梯度下降的算法,但是你并不需要全部掌握,你可以使用Octave提供的库
比如说fminunc你只需要提供所计算的代价函数,每个$\theta$的导数,初始$\theta$即可以使用
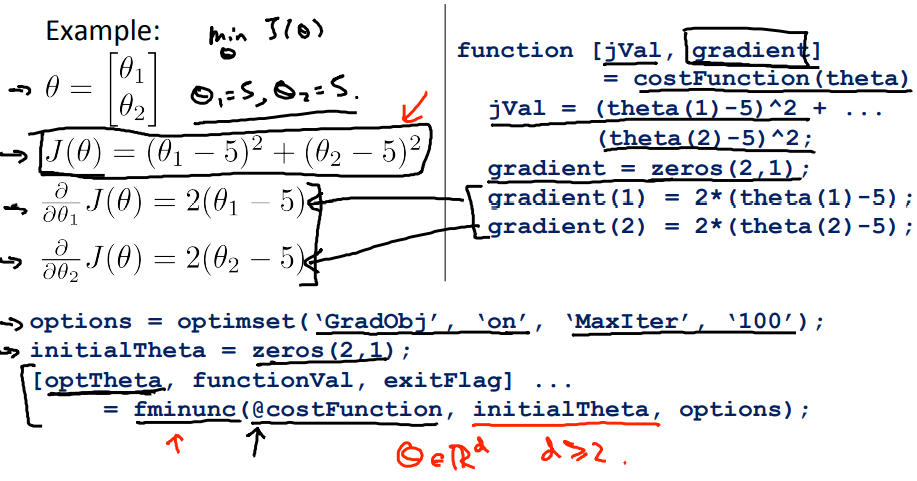
比如对于图上的代价函数$J$,你需要提供一个代价函数costFunction,返回[代价值jVal,每个参数的导数gradient]
设置高级优化函数的参数options,提供初始化的参数initialTheta,函数经过计算会返回[最佳的参数optTheta, 代价函数的值functionVal,是否收敛exitFlag]
多类别分类
有时候需要你区分的类别可能不止2中,可能有3种,4种或更多
比如,病人带着鼻塞来到诊所,你需要区分是没生病,还是着凉还是流感,这里$y=0$代表没生病,$y=1$代表着凉, $y=2$代表流感
对于这种情况,我们可以将3种类型看成2种,进行3次的逻辑回归
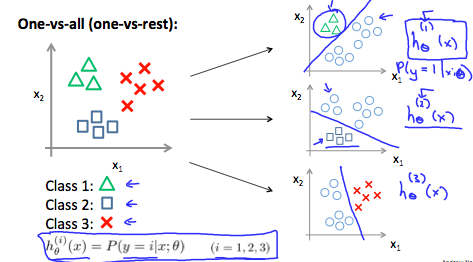
我们每次只看1类,$h_{\theta}^{(i)}(x) = P(y=1|x;\theta)$为为这种情况为1的概率
当我们接收一个新的$x$时,我们对于每个逻辑回归最判断,得出最有可能的概率$\max\limits_{i}h_{\theta}^{(i)}(x)$
过拟合问题
在拟合数据时,为了更好的拟合数据集,我们可能会选择一个很复杂的函数,它对于数据集有很好的效果,但是对于验证集的效果却很差
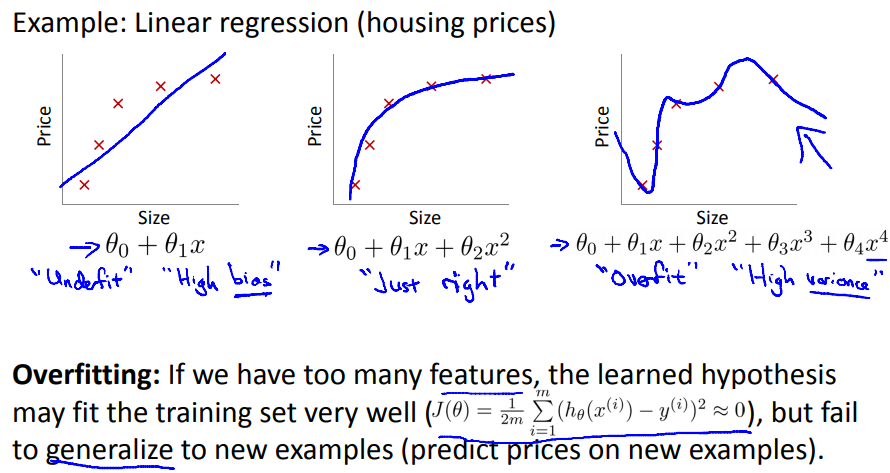
怎么解决
减少特征的数量
- 尽量减少特征的数量
- 通过模型选择算法
正则化
- 保持所有的特征,但是减少$\theta$的量级或是大小
- 当你面对大量的特征时,使用正则化
正则化和代价函数
正则化思想: 每个参数都很小
- 对于很小的参数,我们可以得到更简单的假设模型
- 更不容易出现过拟合的情况
但是我们要怎么决定哪些参数应该去缩小呢,这就要去修改我们的代价函数
这是线性回归的代价函数$J(\theta)=\frac{1}{2m}(h_{\theta}(x^{(i)})-y^{(i)})^2$
我们在后面加入一个新的项用来减小每个$\theta$,$J(\theta)=\frac{1}{2m}[(h_{\theta}(x^{(i)})-y^{(i)})^2 + \lambda\sum\limits_{i=1}^n\theta_{j}^2]$
$\lambda$:正则化参数,控制两个不同目标的取舍,第一个目标就是我们的代价函数,我们想让代价函数尽可能的小,同时第二个目标是$\theta$的和,我们也想让参数的和尽可能的小
正则化线性回归
代价函数发生了改变,那么相对于的,线性回归的梯度下降公式也会发生改变
$Repeat\ \{ \\ \theta_{0} := \theta_{0} - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{0}^{(i)} \\ \theta_{j} := \theta_{j} - \alpha [(\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}) + \frac{\lambda}{m}\theta_j] \\ \}$
因为正则化并没有加入$\theta_0$,所以$\theta_0$需要特殊处理
观察$\theta_j$,我们能可以做一个简单的合并$\theta_j := \theta_j(1-\alpha\frac{\lambda}{m})-\lambda\frac{1}{m}\sum\limits_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}$
正则化正规方程
$X = \begin{bmatrix} (x^{(1)})^T \\ \dots \\ (x^{(m)})^T \end{bmatrix}$ $y=\begin{bmatrix} y^{(1)} \\ \dots \\ y^{(m)} \end{bmatrix}$
正规方程的公式修改后成为:
$\theta = (X^TX + \lambda \begin{bmatrix} 0 & & & \\ & 1 & & \\ & & \ddots \\ & & & 1 \end{bmatrix}_{(n\times1)\times(n\times1)})^{-1}X^Ty$
正则化逻辑回归
逻辑回归的代价函数
$J(\theta)=-[\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2m}\sum\limits_{j=1}^n\theta_j^2$
逻辑回归的梯度下降
$Repeat\ \{ \\ \theta_{0} := \theta_{0} - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{0}^{(i)} \\ \theta_{j} := \theta_{j} - \alpha [(\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}) + \frac{\lambda}{m}\theta_j] \\ \}$
逻辑回归的梯度下降的转换跟线性回归的类似,但是因为$h$函数的不同,它们实际上还是不同的函数
正则化高级优化函数




