多个特征值
对于多个特征的线性回归,我们使用
$m$:代表训练集的大小
$n$:代表特性的数量
$x^{(i)}$:代表第$i$组数据
$x^{(i)}_j$:代表第$i$组数据中的第$j$个特征
对于多个特性的线性回归公式
$h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n$
我们把参数和特征值看成两个向量
$\theta=\begin{bmatrix}\theta_0 \\ \theta_1 \\ \dots \\ \theta_n \end{bmatrix} ,X = \begin{bmatrix}x_0\\ x_1\\ \dots \\x_n \end{bmatrix}(x_0=1),$
那么$h$就可以看成
$h_{\theta}(x) = \theta^{T}X$
多个特征值的梯度下降
线性回归:$h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n=\theta^TX$
代价函数:$J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2$
梯度下降跟原来$n=1$的时形式相同,只不过扩展了一下
梯度下降:$Repeat \{ \\ \theta_j:=\theta_j-\alpha\frac{\alpha}{\alpha\theta_j}J(\theta) \\ \}$
经过求偏导以后梯度下降变为:
$Repeat \{ \\ \theta_j:=\theta_j-\alpha\frac{1}{m}\sum\limits_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j \\ \}$
特征放缩
- 尽量保证多个特征的值都处于一个相近的范围
- 更一般的将特征放缩到$-1\le x_i \le 1$
- 如果一个特征的范围再$-3\le x_i \le 3$是可以接收的
如何特征放缩
一般的使用:$x_i:=\frac{x_i-\mu_i}{s_i}$来进行特征缩放
$\mu_i$:一般表示训练集中特征$i$的平均值
$s_i$:一般表示训练集中特征$i$的范围(最大值-最小值)
$\alpha$的调整
画一个代价函数随着迭代次数的增加,$J(\theta)$的值的变化图,确保$J(\theta)$随着迭代次数的增加而减小,如果不是,就需要考虑是否再减小$\alpha$
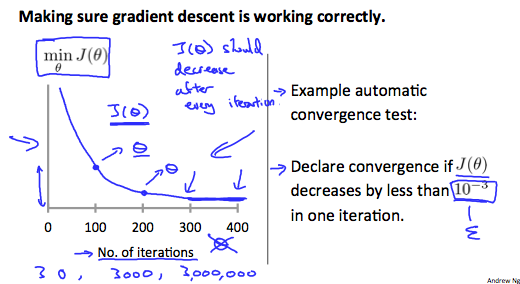
但是如果$\alpha$太小,那么$J(\theta)$的收敛就会变得非常缓慢
收敛
如果$J(\theta)$在一次迭代中减小到小于$E$,那么证明$J(\theta)$已经收敛,$E$是某个小值,如$10^{-3}$。但在实际应用中,这个阈值的选择比较困难。
多项式回归
有时线性回归不足以拟合训练集中的数据,这时我们可以选择多项式回归。
我们可以改变我们的假设函数的行为或曲线,使它成为二次,三次或平方根函数(或任何其他形式)。
例如我们的假设方法是$h_{\theta}(x)=\theta_0+\theta_1x_1$,我们可以根据$x_1$创建附加的特征使其成为二次函数$h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_1^2$或者三次函数$h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_1^2+\theta_3x^3_1$或者我们也可以使用开平方$h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2\sqrt {x_1}$
值得注意的是,任何形式的参数都需要注意特征放缩使其在一个能够接受的范围
正规方程
梯度下降是得到最小代价函数的一种方法,而正规方程也可以得到最小的代价函数,而且是借助数学推导而不是迭代。
在正规方程中,我们显式的对线性回归的每个参数进行偏导,并使它们为0来最小化$J(\theta)$,这使我们在不需要迭代的情况下就能找到最优,正规方程的公式如下
$\theta=(X^TX)^{-1}X^Ty$
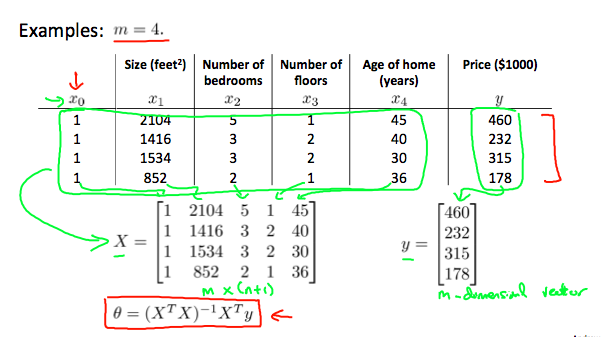
正规方程的特征值不需要进行缩放
梯度下降与正规方程的比较
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择$\alpha$ | 不需要选择$\alpha$ |
| 需要很多次迭代 | 不需要跌代 |
| 复杂度$O(kn^2)$ | 复杂度$O(n^3)$ |
| 在$n$很大时也能很好的工作 | $n$很大时会很慢 |
一般$n\gt 10000$时就不再考虑正规方程了
梯度下降对于很多其他的算法也能有很好的表现,但是正规方程可能并不适合
当$X^TX$不可逆时
在使用Octave时,我们使用$pinv$来求逆,即使你的矩阵不可逆,它也能够求出逆元
但是当$X^TX$不可逆时,我们可能从两个方面找原因
- 特征之间线性相关
- 太多的特征值,而样本又太少
解决上述问题的方法包括删除一个线性相关的特性,如果有太多的特性,删除一个或多个特性。



